动态规划练习

2025-02-21 · 15 分钟阅读 · 算法动态规划 dfs 图论拓扑排序背包问题 ·

复制链接:

文章目录

下面的题目来自洛谷题单【动态规划1】动态规划的引入

解决动态规划问题的三个核心：dp 数组含义、状态转移方程、初始值。

P1216 [IOI 1994] 数字三角形 Number Triangles

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

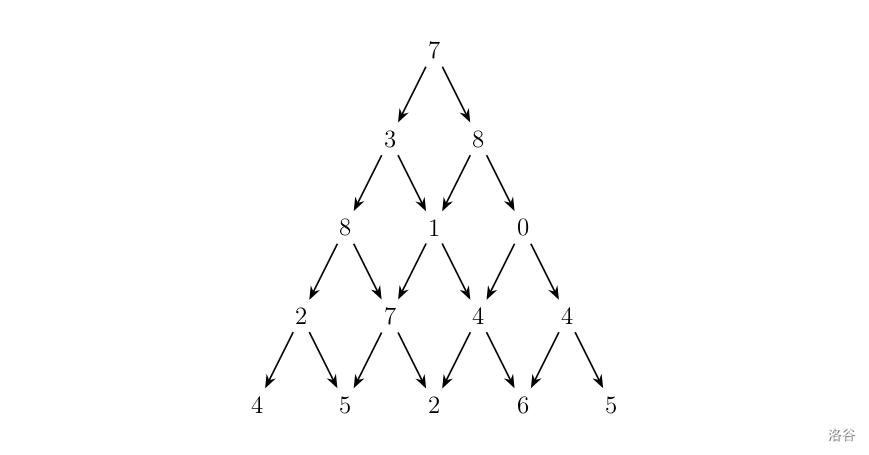
在上面的样例中，从 $7 \to 3 \to 8 \to 7 \to 5$ 的路径产生了最大权值。

输入格式

第一个行一个正整数 $r$ ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

【数据范围】对于 $100%$ 的数据，$1\le r \le 1000$，所有输入在 $[0,100]$ 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

题解

从上到下的最大值和从下到上的最大值是一样的，因此不妨把金字塔倒过来用 DP 求解。例如对于样例中的金字塔，倒过来后就是

用 dp[i][j] 表示走到第 i 行第 j 列时的最大权重，当前位置的最大权重是上方和右上中最大的权重加上当前位置权重，即 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j + 1]) + w[i][j]。

 1r = int(input().strip())
 2pyramid = list()
 3for _ in range(r):
 4    pyramid.append(list(map(int, input().strip().split())))
 5pyramid.reverse()
 6
 7dp = [[0 for _ in range(r)] for _ in range(r)]
 8dp[0] = pyramid[0]
 9for i in range(1, r):
10    for j in range(r - i):
11        dp[i][j] = max(dp[i - 1][j], dp[i - 1][j + 1]) + pyramid[i][j]
12
13print(dp[-1][0])

观察发现当 dp[i][j] 计算完成后，dp[i - 1][j] 不会被重复利用，因此可以使用滚动数组优化。

 1r = int(input().strip())
 2pyramid = list()
 3for _ in range(r):
 4    pyramid.append(list(map(int, input().strip().split())))
 5pyramid.reverse()
 6
 7dp = pyramid[0]
 8for i in range(1, r):
 9    for j in range(r - i):
10        dp[j] = max(dp[j], dp[j + 1]) + pyramid[i][j]
11
12print(dp[0])

动态规划的优化都是基于代码本身做出的优化，而非思路上的优化。

P1115 最大子段和

题目描述

给出一个长度为 $n$ 的序列 $a$，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度 $n$。

第二行有 $n$ 个整数，第 $i$ 个整数表示序列的第 $i$ 个数字 $a_i$。

输出格式

输出一行一个整数表示答案。

输入输出样例 #1

输入 #1

17
22 -4 3 -1 2 -4 3

输出 #1

说明/提示

样例 1 解释

选取 $[3, 5]$ 子段 ${3, -1, 2}$，其和为 $4$。

数据规模与约定

对于 $40%$ 的数据，保证 $n \leq 2 \times 10^3$。
对于 $100%$ 的数据，保证 $1 \leq n \leq 2 \times 10^5$，$-10^4 \leq a_i \leq 10^4$。

题解

要求某一区间的和，自然而然想到用前缀和。因此将题目转换成在前缀和数组中找到两个数，使得后一个数减去前一个数的差最大。

要找到这个两个数，使用两层循环肯定会超时。因此定义 dp[i] 表示前缀和数组的前 i 个数字中出现的最大差值。装填转移方程 dp[i] = max(dp[i - 1], prefex_sum[i] - min_val)，其中 min_val 是动态维护的前缀和数组最小值，初始化为 0；dp[0] 初始化为 prefix_sum[0] 即前缀和数组的第一个数。

 1n = int(input().strip())
 2a = list(map(int, input().strip().split()))
 3prefix_sum = [0] * (n + 1)
 4
 5for i in range(n):
 6    prefix_sum[i + 1] = prefix_sum[i] + a[i]
 7
 8dp = [0] * (n + 1)
 9dp[0] = a[0]
10min_val = 0
11for i in range(1, n + 1):
12    dp[i] = max(dp[i - 1], prefix_sum[i] - min_val)
13    min_val = min(min_val, prefix_sum[i])
14
15print(dp[-1])

P1802 5 倍经验日

题目背景

现在乐斗有活动了！每打一个人可以获得 5 倍经验！absi2011 却无奈的看着那一些比他等级高的好友，想着能否把他们干掉。干掉能拿不少经验的。

题目描述

现在 absi2011 拿出了 $x$ 个迷你装药物（嗑药打人可耻…），准备开始与那些人打了。

由于迷你装药物每个只能用一次，所以 absi2011 要谨慎的使用这些药。悲剧的是，用药量没达到最少打败该人所需的属性药药量，则打这个人必输。例如他用 $2$ 个药去打别人，别人却表明 $3$ 个药才能打过，那么相当于你输了并且这两个属性药浪费了。

现在有 $n$ 个好友，给定失败时可获得的经验、胜利时可获得的经验，打败他至少需要的药量。

要求求出最大经验 $s$，输出 $5s$。

输入格式

第一行两个数，$n$ 和 $x$。

后面 $n$ 行每行三个数，分别表示失败时获得的经验 $\mathit{lose}_i$，胜利时获得的经验 $\mathit{win}_i$ 和打过要至少使用的药数量 $\mathit{use}_i$。

输出格式

一个整数，最多获得的经验的五倍。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

【Hint】

五倍经验活动的时候，absi2011 总是吃体力药水而不是这种属性药。

【数据范围】

对于 $10%$ 的数据，保证 $x=0$。
对于 $30%$ 的数据，保证 $0\le n\le 10$，$0\le x\le 20$。
对于 $60%$ 的数据，保证 $0\le n,x\le 100$， $10<lose_i,win_i\le 100$，$0\le use_i\le 5$。
对于 $100%$ 的数据，保证 $0\le n,x\le 10^3$，$0<lose_i\le win_i\le 10^6$，$0\le use_i\le 10^3$。

【题目来源】

fight.pet.qq.com

absi2011 授权题目

题解

定义 dp[i][j] 表示攻击前 i 个人且最多只用 j 个药时能获得的经验总和。如果选择不攻击第 i 个人，那么获得的经验是 dp[i - 1][j] + lose[i]，如果选择攻击第 i 个人，那么获得的经验是 dp[i - 1][j - use[i]] + win[i]。当然，如果 j < use[i] 那就只能选择不攻击。最后计算出来的结果要乘 5。

 1n, x = map(int, input().strip().split())
 2lose, win, use = [0], [0], [0]
 3for _ in range(n):
 4    li, wi, ui = map(int, input().strip().split())
 5    lose.append(li)
 6    win.append(wi)
 7    use.append(ui)
 8
 9dp = [[0 for _ in range(x + 1)] for _ in range(n + 1)]
10for i in range(1, n + 1):
11    for j in range(x + 1):
12        if j < use[i]:
13            dp[i][j] = dp[i - 1][j] + lose[i]
14        else:
15            dp[i][j] = max(dp[i - 1][j] + lose[i], dp[i - 1][j - use[i]] + win[i])
16
17print(dp[n][x] * 5)

回过头来看，这就是一个带有保底的 01 背包问题。不管是否选择打第 i 个人，都能获得 lose[i] 的得分，而总药量 x 就是背包容量。按照 01 背包的方式来优化代码：

1n, x = map(int, input().strip().split())
2guarantee = 0
3dp = [0] * (x + 1)
4for _ in range(n):
5    lose, win, use = map(int, input().strip().split())
6    guarantee += lose
7    for j in range(use, x + 1)[::-1]:
8        dp[j] = max(dp[j], dp[j - use] + (win - lose))
9print((dp[-1] + guarantee) * 5)

P1002 [NOIP 2002 普及组] 过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$，同样马的位置坐标是需要给出的。

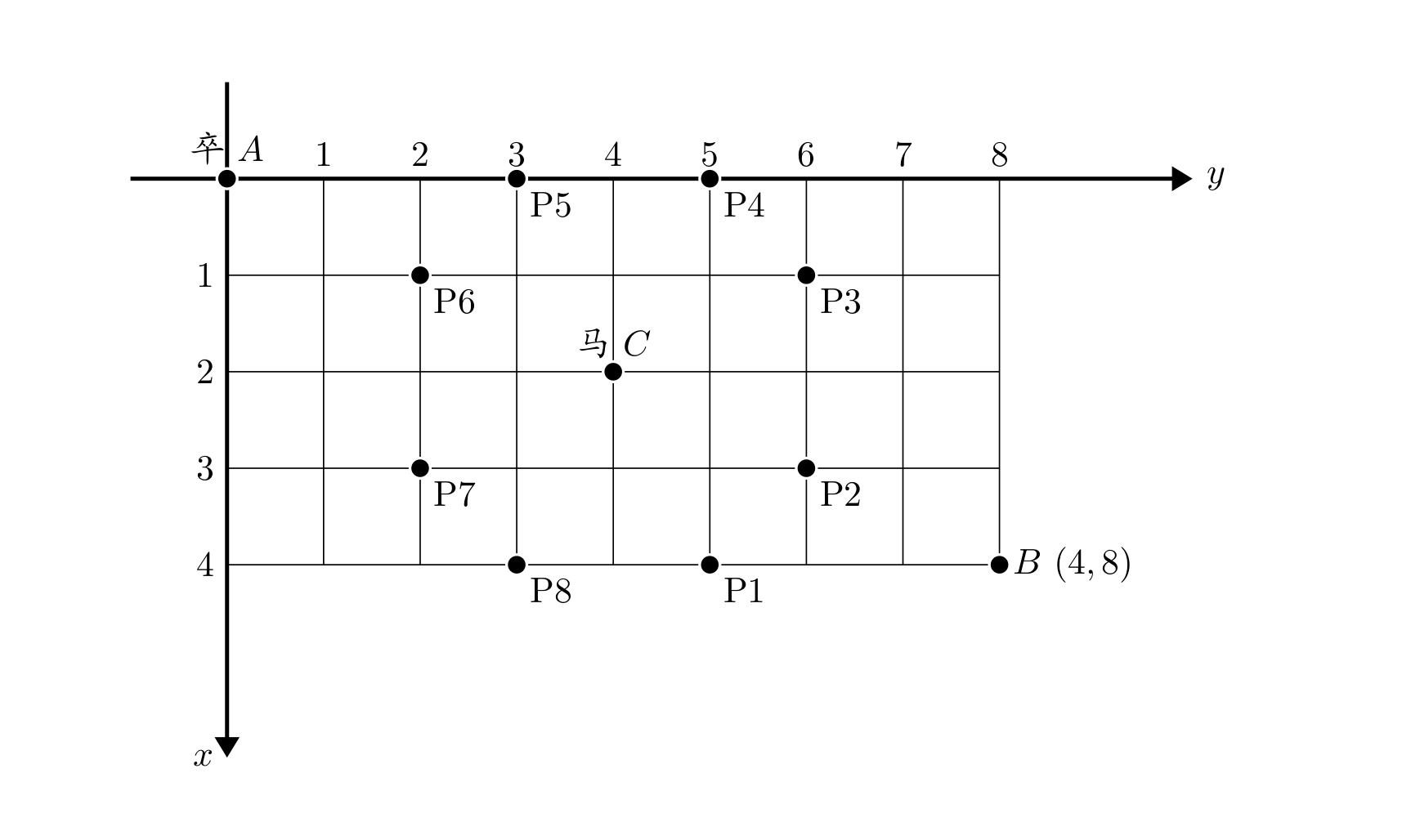
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例 #1

输入 #1

16 6 3 3

输出 #1

说明/提示

对于 $100 %$ 的数据，$1 \le n, m \le 20$，$0 \le$ 马的坐标 $\le 20$。

【题目来源】

NOIP 2002 普及组第四题

题解

小学时手自笔录做过这类题目。令 dp[i][j] 表示走到 $(i,j)$ 位置时的方法数。为了方便计算（以及写代码），不妨将 dp 所有数初始化为 1，而不能走的位置初始化为 0。不过需要注意的是，如果 dp[i][0] 或者 dp[0][j] 不可通行，那么其下方或右侧全部格子都应当改为 0。

 1n, m, x, y = map(int, input().strip().split())
 2directions = ((-1, -2), (-2, -1), (-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2), (0, 0))
 3dp = [[1 for _ in range(m + 1)] for _ in range(n + 1)]
 4
 5for d in directions:
 6    dx, dy = d
 7    nx, ny = x + dx, y + dy
 8    if 0 <= nx <= n and 0 <= ny <= m:
 9        dp[nx][ny] = 0
10
11blocked_row = False
12for i in range(n + 1):
13    if dp[i][0] == 0:
14        blocked_row = True
15        continue
16    if blocked_row:
17        dp[i][0] = 0
18
19blocked_col = False
20for j in range(m + 1):
21    if dp[0][j] == 0:
22        blocked_col = True
23        continue
24    if blocked_col:
25        dp[0][j] = 0
26
27for i in range(1, n + 1):
28    for j in range(1, m + 1):
29        if dp[i][j] == 0:
30            continue
31        dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
32
33print(dp[n][m])

这道题也可以用深搜，不过需要带记忆化搜索，动态保存数据方案数，以避在某个位置重复计算。

 1n, m, x, y = map(int, input().strip().split())
 2directions = ((-1, -2), (-2, -1), (-2, 1), (-1, 2), (1, 2), (2, 1), (2, -1), (1, -2), (0, 0))
 3blocked = {(x + dx, y + dy): True for dx, dy in directions}
 4
 5
 6def dfs(i, j, memo=dict()):
 7    if i == n and j == m:
 8        return 1
 9
10    if memo.get((i, j), False):
11        return memo[(i, j)]
12
13    count = 0
14    if not blocked.get((i + 1, j), False) and i < n:
15        count += dfs(i + 1, j)
16    if not blocked.get((i, j + 1), False) and j < m:
17        count += dfs(i, j + 1)
18
19    memo[(i, j)] = count
20    return count
21
22
23print(dfs(0, 0))

如果我将 memo 改为一个二维数组而非字典，那岂不是还是动态规划。

P2196 [NOIP 1996 提高组] 挖地雷

题目描述

在一个地图上有 $N\ (N \le 20)$ 个地窖，每个地窖中埋有一定数量的地雷。同时，给出地窖之间的连接路径。当地窖及其连接的数据给出之后，某人可以从任一处开始挖地雷，然后可以沿着指出的连接往下挖（仅能选择一条路径），当无连接时挖地雷工作结束。设计一个挖地雷的方案，使某人能挖到最多的地雷。

输入格式

有若干行。

第 $1$ 行只有一个数字，表示地窖的个数 $N$。

第 $2$ 行有 $N$ 个数，分别表示每个地窖中的地雷个数。

第 $3$ 行至第 $N+1$ 行表示地窖之间的连接情况：

第 $3$ 行有 $n-1$ 个数（$0$ 或 $1$），表示第一个地窖至第 $2$ 个、第 $3$ 个 $\dots$ 第 $n$ 个地窖有否路径连接。如第 $3$ 行为 $11000\cdots 0$，则表示第 $1$ 个地窖至第 $2$ 个地窖有路径，至第 $3$ 个地窖有路径，至第 $4$ 个地窖、第 $5$ 个 $\dots$ 第 $n$ 个地窖没有路径。

第 $4$ 行有 $n-2$ 个数，表示第二个地窖至第 $3$ 个、第 $4$ 个 $\dots$ 第 $n$ 个地窖有否路径连接。

……

第 $n+1$ 行有 $1$ 个数，表示第 $n-1$ 个地窖至第 $n$ 个地窖有否路径连接。（为 $0$ 表示没有路径，为 $1$ 表示有路径）。

输出格式

第一行表示挖得最多地雷时的挖地雷的顺序，各地窖序号间以一个空格分隔，不得有多余的空格。

第二行只有一个数，表示能挖到的最多地雷数。

输入输出样例 #1

输入 #1

15
210 8 4 7 6
31 1 1 0
40 0 0
51 1
61

输出 #1

11 3 4 5
227

说明/提示

【题目来源】

NOIP 1996 提高组第三题

题解

这道题相当于给出一个有向图的邻接矩阵，将矩阵存储进 adj_mat 中，其中 adj_mat[i][j] 表示是否存在 $i\rightarrow j$ 的路径。

最容易想到的做法是深搜，遍历每一个节点作为起始节点，找出各种情况下的最大值。

 1n = int(input().strip())
 2mines = list(map(int, input().strip().split()))
 3adj_mat = list()
 4for i in range(n - 1):
 5    adj_mat.append([0] * (i + 1) + list(map(int, input().strip().split())))
 6adj_mat.append([0] * (n))
 7
 8
 9def dfs(i, path):
10    if i == n - 1:
11        return mines[i], [str(i + 1)]
12
13    max_val = 0
14    max_path = list()
15    for j in range(i + 1, n):
16        if adj_mat[i][j]:
17            m, p = dfs(j, path)
18            if m > max_val:
19                max_val = m
20                max_path = p
21    return max_val + mines[i], [str(i + 1)] + max_path
22
23
24max_val = 0
25max_path = list()
26for i in range(n):
27    m, p = dfs(i, list())
28    if m > max_val:
29        max_val = m
30        max_path = p
31
32print(" ".join(max_path))
33print(max_val)

当然这道题也可以用动态规划解决。令数组 dp[i] 表示走到第 i 个地窖时能挖到的最大地雷数量以及相对应的路径。到达每一个地窖时，遍历前面每一个能够到达它的地窖，找出其中的最大值再加上当前地窖的地雷数，就是走到当前地窖能获得的最大值。而且使用动态规划不需要讨论初始节点。

 1n = int(input().strip())
 2mines = list(map(int, input().strip().split()))
 3adj_mat = list()
 4for i in range(n - 1):
 5    adj_mat.append([0] * (i + 1) + list(map(int, input().strip().split())))
 6adj_mat.append([0] * (n))
 7
 8dp = [[0, list()] for _ in range(n)]
 9path = list()
10for i in range(n):
11    val = 0
12    p = list()
13    for j in range(n):
14        if adj_mat[j][i] and dp[j][0] > val:
15            val = dp[j][0]
16            p = dp[j][1]
17    dp[i][0] = val + mines[i]
18    dp[i][1] = p + [str(i + 1)]
19
20max_val = 0
21max_path = list()
22for v, p in dp:
23    if v > max_val:
24        max_val = v
25        max_path = p
26
27print(" ".join(max_path))
28print(max_val)

P1434 [SHOI2002] 滑雪

题目描述

Michael 喜欢滑雪。这并不奇怪，因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子：

11   2   3   4   5
216  17  18  19  6
315  24  25  20  7
414  23  22  21  8
513  12  11  10  9

一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度会减小。在上面的例子中，一条可行的滑坡为 $24-17-16-1$（从 $24$ 开始，在 $1$ 结束）。当然 $25$－$24$－$23$－$\ldots$－$3$－$2$－$1$ 更长。事实上，这是最长的一条。

输入格式

输入的第一行为表示区域的二维数组的行数 $R$ 和列数 $C$。下面是 $R$ 行，每行有 $C$ 个数，代表高度(两个数字之间用 $1$ 个空格间隔)。

输出格式

输出区域中最长滑坡的长度。

输入输出样例 #1

输入 #1

15 5
21 2 3 4 5
316 17 18 19 6
415 24 25 20 7
514 23 22 21 8
613 12 11 10 9

输出 #1

说明/提示

对于 $100%$ 的数据，$1\leq R,C\leq 100$。

题解

一看到这道题我就感觉来者不善。如果需要使用动态规划来解决，定义出 dp 数组很容易，即 dp[i][j] 表示在 $(i,j)$ 位置上时可以上滑的最大长度（下滑上滑是一样的，为了方便写代码应该描述成上滑，原因下面会提），但是如何遍历这个数组就有些麻烦了。因为题目允许向四个方向自由移动，那么遍历时就应该按照实际能够经过的顺序处理每一个位置。如果地形在任意位置都是左高右低，上高下低就可以按照一般两层循环的方式来遍历，但是在这道题中无法实现。

为了解决这个问题，不妨按照地势高低顺序来遍历。利用 heapq 模块实现最小堆（默认实现最小堆，若要实现最大堆可使用相反数），将地形数据存储到最小堆中，这样就可以按照从低到高的顺序遍历 dp 数组。

heapq 模块使用介绍

heapq — Heap queue algorithm

 1import heapq
 2
 3
 4row, col = map(int, input().strip().split())
 5height = list()
 6heap = list()
 7for i in range(row):
 8    c = list(map(int, input().strip().split()))
 9    height.append(c)
10    for j in range(col):
11        heapq.heappush(heap, (c[j], (i, j)))
12
13directions = ((-1, 0), (0, 1), (1, 0), (0, -1))
14dp = [[0 for _ in range(col)] for _ in range(row)]
15while heap:
16    h, (i, j) = heapq.heappop(heap)
17    max_l = 0
18    for d in directions:
19        di, dj = d
20        ni, nj = i + di, j + dj
21        if 0 <= ni < row and 0 <= nj < col and height[ni][nj] < h:
22            max_l = max(max_l, dp[ni][nj])
23    dp[i][j] = max_l + 1
24
25max_l = 0
26for i in range(row):
27    for j in range(col):
28        max_l = max(max_l, dp[i][j])
29print(max_l)

heapq 不支持自定义 key 排序，因此需要将 key 和 value 同时存储进一个 tuple 中，并且将 key 作为首元素，即代码中的 heapq.heappush(heap, (c[j], (i, j)))。

这道题也可以用深搜解决，尝试将每一个节点作为起点找出最长路径。不过必须要用记忆化搜索，否则会超时。

 1row, col = map(int, input().strip().split())
 2height = list()
 3for _ in range(row):
 4    height.append(list(map(int, input().strip().split())))
 5directions = ((-1, 0), (0, 1), (1, 0), (0, -1))
 6memo = [[0 for _ in range(col)] for _ in range(row)]
 7
 8
 9def dfs(i, j, memo):
10    if memo[i][j]:
11        return memo[i][j]
12
13    count = 1
14    for di, dj in directions:
15        ni, nj = i + di, j + dj
16        if 0 <= ni < row and 0 <= nj < col and height[ni][nj] > height[i][j]:
17            count = max(dfs(ni, nj, memo) + 1, count)
18
19    memo[i][j] = count
20    return count
21
22
23max_count = 0
24for i in range(row):
25    for j in range(col):
26        m = memo[:]
27        max_count = max(max_count, dfs(i, j, m))
28print(max_count)

奇怪的是这道题深搜写法的时空性能均优于 DP 写法。

P4017 最大食物链计数

题目背景

你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

Delia 非常急，所以你只有 $1$ 秒的时间。

由于这个结果可能过大，你只需要输出总数模上 $80112002$ 的结果。

输入格式

第一行，两个正整数 $n、m$，表示生物种类 $n$ 和吃与被吃的关系数 $m$。

接下来 $m$ 行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式

一行一个整数，为最大食物链数量模上 $80112002$ 的结果。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

各测试点满足以下约定：

测试点编号	n	m
1,2	≤40	≤400
3,4	≤100	≤2000
5,6	≤1000	≤60000
7,8	≤2000	≤200000
9,10	≤5000	≤500000

【补充说明】

数据中不会出现环，满足生物学的要求。（感谢 @AKEE ）

题解

这道题依然可以使用动态规划解决。令 dp[i] 表示以第 i 个生物为终点时的链数，dp[i] 的值为其全部前驱节点链数之和。这道题真正容易出错的点在于遍历节点的顺序。

如果要计算某个节点的链数，则必须先处理其前驱节点，因此对图做拓扑排序得到遍历节点的顺序。

拓扑排序介绍

通过拓扑序处理节点能够保证每一个节点的前驱节点都一定先于这个节点处理。因此可以得到下面的代码：

 1from collections import defaultdict, deque
 2
 3
 4graph = defaultdict(list)
 5in_degree = defaultdict(int)
 6n, m = map(int, input().strip().split())
 7for _ in range(m):
 8    a, b = map(int, input().strip().split())
 9    graph[a].append(b)
10    in_degree[b] += 1
11
12dp = [0] * (n + 1)
13queue = deque()
14
15for node in range(1, n + 1):
16    if in_degree[node] == 0:
17        queue.append(node)
18        dp[node] = 1
19
20while queue:
21    node = queue.popleft()
22    for dest in graph[node]:
23        dp[dest] += dp[node]
24        in_degree[dest] -= 1
25        if in_degree[dest] == 0:
26            queue.append(dest)
27
28ans = 0
29for i in range(1, n + 1):
30    if not graph[i]:
31        ans += dp[i]
32print(ans % 80112002)

单独用于拓扑排序的代码如下：

 1def topo_sort(graph: defaultdict):
 2    in_degree = defaultdict(int)
 3    for node in range(1, n + 1):
 4        for dest in graph[node]:
 5            in_degree[dest] += 1
 6
 7    queue = deque()
 8    for node in range(1, n + 1):
 9        if in_degree[node] == 0:
10            queue.append(node)
11
12    topo = list()
13    while queue:
14        node = queue.popleft()
15        topo.append(node)
16        for dest in graph[node]:
17            in_degree[dest] -= 1
18            if in_degree[dest] == 0:
19                queue.append(dest)
20
21    return topo

参数 graph 为存储的键值对为节点及其后继节点的列表。in_dgree 字典用于维护当前图中每一个节点的入度。当节点的入度为 0 时，节点入队，并且与其所有出边都被删除，即该节点的后继节点的入度减去 1。随后重复该操作，如果图有向无环，则一定能构造出节点的拓扑序列。

P1077 [NOIP 2012 普及组] 摆花

题目描述

小明的花店新开张，为了吸引顾客，他想在花店的门口摆上一排花，共 $m$ 盆。通过调查顾客的喜好，小明列出了顾客最喜欢的 $n$ 种花，从 $1$ 到 $n$ 标号。为了在门口展出更多种花，规定第 $i$ 种花不能超过 $a_i$ 盆，摆花时同一种花放在一起，且不同种类的花需按标号的从小到大的顺序依次摆列。

试编程计算，一共有多少种不同的摆花方案。

输入格式

第一行包含两个正整数 $n$ 和 $m$，中间用一个空格隔开。

第二行有 $n$ 个整数，每两个整数之间用一个空格隔开，依次表示 $a_1,a_2, \cdots ,a_n$。

输出格式

一个整数，表示有多少种方案。注意：因为方案数可能很多，请输出方案数对 $10^6+7$ 取模的结果。

输入输出样例 #1

输入 #1

12 4
23 2

输出 #1

说明/提示

【数据范围】

对于 $20%$ 数据，有 $0<n \le 8,0<m \le 8,0 \le a_i \le 8$。

对于 $50%$ 数据，有 $0<n \le 20,0<m \le 20,0 \le a_i \le 20$。

对于 $100%$ 数据，有 $0<n \le 100,0<m \le 100,0 \le a_i \le 100$。

NOIP 2012 普及组第三题

题解

感觉这道题的搜索思路做比动态规划更容易理解一些。当然，如果要用搜索则必须要使用记忆化搜索，不然肯定会超时。

 1from collections import defaultdict
 2
 3MOD = 10**6 + 7
 4
 5n, m = map(int, input().strip().split())
 6a = tuple(map(int, input().strip().split()))
 7
 8
 9def dfs(count, kinds, memo):
10
11    if memo[(count, kinds)] != -1:
12        return memo[(count, kinds)]
13
14    if count == m:
15        return 1
16    if count > m:
17        return 0
18    if kinds >= n:
19        return 0
20
21    current = 0
22    for i in range(0, a[kinds] + 1):
23        current += dfs(count + i, kinds + 1, memo)
24        current %= MOD
25    memo[(count, kinds)] = current
26    return current
27
28
29print(dfs(0, 0, defaultdict(lambda: -1)))

这里面 defaultdict(lambda: -1) 的意思是以 -1 作为这个 defaultdict 的默认值，因为其构造方法只接收函数作为参数，所以使用 lambda 定义函数。

这道题有些类似与多重背包问题，但是这道题要求的是方案数而非最大价值。令 dp[i][j] 表示只考虑前 i 种花且最多放 j 盆花时的方法数。因为花的摆放有顺序，因此 dp[i][j] 表示的方法数是在最后 k 个位置摆放第 i 种花的方法数之和，其中 $0\leq k\leq a_i$。

 1n, m = map(int, input().strip().split())
 2a = (0,) + tuple(map(int, input().strip().split()))
 3MOD = 10**6 + 7
 4dp = [[0 for _ in range(m + 1)] for _ in range(n + 1)]
 5dp[0][0] = 1
 6for i in range(1, n + 1):
 7    for j in range(m + 1):
 8        dp[i][j] = sum(dp[i - 1][max(0, j - a[i]): j + 1])
 9        dp[i][j] %= MOD
10print(dp[-1][-1] % MOD)

观察代码，每一个 dp[i][j] 都只与其上一行左侧的数据有关，因此可以使用滚动数组优化降低空间消耗。因为每一个 dp[i][j] 与其左上方的值有关，因此内循环需要从右向左遍历。

 1n, m = map(int, input().strip().split())
 2a = (0,) + tuple(map(int, input().strip().split()))
 3MOD = 10**6 + 7
 4dp = [0 for _ in range(m + 1)]
 5dp[0] = 1
 6for i in range(1, n + 1):
 7    for j in range(m + 1)[::-1]:
 8        dp[j] = sum(dp[max(0, j - a[i]) : j + 1])
 9        dp[j] %= MOD
10print(dp[-1] % MOD)

P3842 [TJOI2007] 线段

题目描述

在一个 $n \times n$ 的平面上，在每一行中有一条线段，第 $i$ 行的线段的左端点是$(i, L_{i})$，右端点是$(i, R_{i})$。

你从 $(1,1)$ 点出发，要求沿途走过所有的线段，最终到达 $(n,n)$ 点，且所走的路程长度要尽量短。

更具体一些说，你在任何时候只能选择向下走一步（行数增加 $1$）、向左走一步（列数减少 $1$）或是向右走一步（列数增加 $1$）。当然，由于你不能向上行走，因此在从任何一行向下走到另一行的时候，你必须保证已经走完本行的那条线段。

输入格式

第一行有一个整数 $n$。

以下 $n$ 行，在第 $i$ 行（总第 $(i+1)$ 行）的两个整数表示 $L_i$ 和 $R_i$。

输出格式

仅包含一个整数，你选择的最短路程的长度。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

我们选择的路线是

1 (1, 1) (1, 6)
2 (2, 6) (2, 3)
3 (3, 3) (3, 1)
4 (4, 1) (4, 2)
5 (5, 2) (5, 6)
6 (6, 6) (6, 4) (6, 6)

不难计算得到，路程的总长度是 $24$。

对于 $100%$ 的数据中，$n \le 2 \times 10^4$，$1 \le L_i \le R_i \le n$。

题解

最开始看到“最短路径”几个字，还以为可以用广搜，但是仔细读题感觉用广搜做还是有些困难。

定义 dp[i][0] 和 dp[i][1] 分别表示走到第 i 行的左端点和右端点且已经走完整条线段时的最短路径长度。状态转移一共有四种情况：上一行左端点到本行左端点、上一行右端点到本行左端点、上一行左端点到本行右端点、上一行右端点到本行右端点。无论目的地是本行的左端点还是右端点，一定要先走过本行的另一个端点。假设本行的左右端点分别用 $l,r$ 表示，上一行的左右端点分别用 $l',r'$ 表示，则前面提到的四种情况可以分别表示为 $l'\rightarrow r\rightarrow l$、$r'\rightarrow r\rightarrow l$、$l'\rightarrow l\rightarrow r$、$r'\rightarrow l\rightarrow r$。dp[i][0] 取前两者最小值，dp[i][1] 取后两者最小值，当然还要加上纵向距离 1。因为出发点是 $(1,1)$，即可以假设第 0 行的左右端点都为 1，即当 $i=1$时，$l'=r'=1$，dp[0] = [1, 1]。

 1n = int(input().strip())
 2dp = [[0, 0] for _ in range(n + 1)]
 3l_, r_ = 1, 1
 4for i in range(1, n + 1):
 5    l, r = map(int, input().strip().split())
 6    d = r - l
 7    dp[i][0] = min(abs(r - l_) + d + dp[i - 1][0], abs(r - r_) + d + dp[i - 1][1]) + 1
 8    dp[i][1] = min(abs(l - l_) + d + dp[i - 1][0], abs(l - r_) + d + dp[i - 1][1]) + 1
 9    l_, r_ = l, r
10
11print(min(dp[-1][0] + (n - l), dp[-1][1] + (n - r)) - 1)

这道题用滚动数组优化不太现实，因为计算 dp[i][0] 和 dp[i][1] 时都需要用到 dp[i - 1][0] 和 dp[i - 1][1]。不过基于 Python 的逆天特性，dp[i][0] 和 dp[i][1] 可以同时计算而且互不影响，也就是将其写进一行。

 1n = int(input().strip())
 2dp = [0, 0]
 3l_, r_ = 1, 1
 4for i in range(n):
 5    l, r = map(int, input().strip().split())
 6    d = r - l
 7    dp[0], dp[1] = (min(abs(r - l_) + d + dp[0], abs(r - r_) + d + dp[1]) + 1, min(abs(l - l_) + d + dp[0], abs(l - r_) + d + dp[1]) + 1)
 8    l_, r_ = l, r
 9
10print(min(dp[0] + (n - l), dp[1] + (n - r)) - 1)

优化效果不是很好，而且时空消耗反而更高了（？）

P1064 [NOIP 2006 提高组] 金明的预算方案

题目描述

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 $n$ 元钱就行”。今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

主件	附件
电脑	打印机，扫描仪
书柜	图书
书桌	台灯，文具
工作椅	无

如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件可以有 $0$ 个、$1$ 个或 $2$ 个附件。每个附件对应一个主件，附件不再有从属于自己的附件。金明想买的东西很多，肯定会超过妈妈限定的 $n$ 元。于是，他把每件物品规定了一个重要度，分为 $5$ 等：用整数 $1 \sim 5$ 表示，第 $5$ 等最重要。他还从因特网上查到了每件物品的价格（都是 $10$ 元的整数倍）。他希望在不超过 $n$ 元的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 $j$ 件物品的价格为 $v_j$，重要度为 $w_j$，共选中了 $k$ 件物品，编号依次为 $j_1,j_2,\dots,j_k$，则所求的总和为：

$$v_{j_1} \times w_{j_1}+v_{j_2} \times w_{j_2}+ \dots +v_{j_k} \times w_{j_k}$$

请你帮助金明设计一个满足要求的购物单。

输入格式

第一行有两个整数，分别表示总钱数 $n$ 和希望购买的物品个数 $m$。

第 $2$ 到第 $(m + 1)$ 行，每行三个整数，第 $(i + 1)$ 行的整数 $v_i$，$p_i$，$q_i$ 分别表示第 $i$ 件物品的价格、重要度以及它对应的的主件。如果 $q_i=0$，表示该物品本身是主件。

输出格式

输出一行一个整数表示答案。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

数据规模与约定

对于全部的测试点，保证 $1 \leq n \leq 3.2 \times 10^4$，$1 \leq m \leq 60$，$0 \leq v_i \leq 10^4$，$1 \leq p_i \leq 5$，$0 \leq q_i \leq m$，答案不超过 $2 \times 10^5$。

NOIP 2006 提高组第二题

题解

每一个主件最多带有 $2$ 个附件，所以每一个主件都有五种情况，每种情况与其所对应的价格-期望分别为

啥都不选，$(0,0)$；
只选主件，$(v_{main}, v_{main}\times p_{main})$；
选主件和附件一（如果存在），$(v_{main}+v_{attach1}, v_{main}\times p_{main}+v_{attach1}\times p_{attach1})$；
选主件和附件二（如果存在），$(v_{main}+v_{attach2}, v_{main}\times p_{main}+v_{attach2}\times p_{attach2})$；
选主件和两个附件（如果存在），$(v_{main}+v_{attach1}+v_{attach2}, v_{main}\times p_{main}+v_{attach1}\times p_{attach1}+v_{attach2}\times p_{attach2})$；

以上五种情况相互冲突，只能选则一种。此时，这道依赖背包问题就被转换成了分组背包问题。

另外由于题目给出的金额都是 $10$ 的倍数，因此可以在处理时将所有金额都除以 $10$，最后再乘回去以降低时空消耗。

下面是使用滚动数组优化过的代码：

 1from collections import defaultdict
 2
 3n, m = map(int, input().strip().split(" "))
 4n //= 10
 5
 6main = list()
 7attach = defaultdict(list)
 8for i in range(1, m + 1):
 9    v, p, q = map(int, input().strip().split(" "))
10    v //= 10
11    if q == 0:
12        main.append((v, p, i))
13    else:
14        attach[q].append((v, p))
15
16dp = [0] * (n + 1)
17for m in main:
18    v_main, p_main, idx = m
19    atch = attach[idx]
20    comb = list()
21    comb.append((0, 0))
22    comb.append((v_main, v_main * p_main))
23    if len(atch) >= 1:
24        v_atch, p_atch = atch[0]
25        comb.append((v_main + v_atch, v_main * p_main + v_atch * p_atch))
26    if len(atch) == 2:
27        v_atch, p_atch = atch[1]
28        comb.append((v_main + v_atch, v_main * p_main + v_atch * p_atch))
29    if len(atch) == 2:
30        v_atch1, p_atch1 = atch[0]
31        v_atch2, p_atch2 = atch[1]
32        comb.append((v_main + v_atch1 + v_atch2, v_main * p_main + v_atch1 * p_atch1 + v_atch2 * p_atch2))
33
34    for j in range(0, n + 1)[::-1]:
35        for v, val in comb:
36            if j >= v:
37                dp[j] = max(dp[j], dp[j - v] + val)
38
39print(dp[-1] * 10)

在输入数据中某些附件的数据可能先于其主件数据输入，故需要使用 defaultdict 存储附件信息，否则会 RE。