搜索练习

2025-02-04 · 27 分钟阅读 · 算法 dfs bfs ·

复制链接:

文章目录

深度优先搜索适合用于查找路径、解决组合问题，缺点是递归调用的时间复杂度高。
广度优先搜索适合用于找最短路径，缺点是空间复杂度高。

[NOIP2001 普及组] 求先序排列

题目描述

给出一棵二叉树的中序与后序排列。求出它的先序排列。（约定树结点用不同的大写字母表示，且二叉树的节点个数 $ \le 8$）。

输入格式

共两行，均为大写字母组成的字符串，表示一棵二叉树的中序与后序排列。

输出格式

共一行一个字符串，表示一棵二叉树的先序。

样例 #1

样例输入 #1

1BADC
2BDCA

样例输出 #1

1ABCD

提示

【题目来源】

NOIP 2001 普及组第三题

题解

中序遍历是以左->中->右的顺序遍历树，后续遍历是以左->右->中的顺序遍历树。根据定义我们可以知道以下规律：

后序遍历的最后一个节点一定是根节点，对子树同样成立
中序遍历左子节点一定在根节点前，根节点一定在右子节点前，对子树同样成立
后序遍历左子节点一定在右子节点前，对子树同样成立

随后可以按照这些规律设计算法，还原一颗二叉树：

从后向前读取后序遍历字符串，每一个字符都是某个树的根节点
在中序遍历字符串中找到这个根节点字符，这个字符前面的 n 个字符都属于左子树，后面的 m 个字符都属于右子树
后序遍历字符串的前 n 个字符属于左子树，紧接着的 m 个字符属于右子树
按照上述规律处理子树

 1class Node:
 2
 3    def __init__(self, left=None, right=None, value=str()):
 4        self.left = left
 5        self.right = right
 6        self.value = value
 7
 8
 9def dfs(inorder, postorder):
10    if not postorder:
11        return None
12    node = Node()
13    root = postorder[-1]
14    node.value = root
15    index = inorder.index(root)
16    node.left = dfs(inorder[:index], postorder[:index])
17    node.right = dfs(inorder[index + 1 :], postorder[index:-1])
18    return node
19
20
21def to_list(t, res=None):
22    if res is None:
23        res = list()
24    if not t:
25        return res
26    res.append(t.value)
27    to_list(t.left, res)
28    to_list(t.right, res)
29    return res
30
31
32def main():
33    inorder = input().strip()
34    postorder = input().strip()
35    tree = dfs(inorder, postorder)
36    print("".join(to_list(tree)))
37
38
39if __name__ == "__main__":
40    main()

下面的题目来自洛谷题单【算法1-7】搜索

kkksc03考前临时抱佛脚

题目背景

kkksc03 的大学生活非常的颓废，平时根本不学习。但是，临近期末考试，他必须要开始抱佛脚，以求不挂科。

题目描述

这次期末考试，kkksc03 需要考 $4$ 科。因此要开始刷习题集，每科都有一个习题集，分别有 $s_1,s_2,s_3,s_4$ 道题目，完成每道题目需要一些时间，可能不等（$A_1,A_2,\ldots,A_{s_1}$，$B_1,B_2,\ldots,B_{s_2}$，$C_1,C_2,\ldots,C_{s_3}$，$D_1,D_2,\ldots,D_{s_4}$）。

kkksc03 有一个能力，他的左右两个大脑可以同时计算 $2$ 道不同的题目，但是仅限于同一科。因此，kkksc03 必须一科一科的复习。

由于 kkksc03 还急着去处理洛谷的 bug，因此他希望尽快把事情做完，所以他希望知道能够完成复习的最短时间。

输入格式

本题包含 $5$ 行数据：第 $1$ 行，为四个正整数 $s_1,s_2,s_3,s_4$。

第 $2$ 行，为 $A_1,A_2,\ldots,A_{s_1}$ 共 $s_1$ 个数，表示第一科习题集每道题目所消耗的时间。

第 $3$ 行，为 $B_1,B_2,\ldots,B_{s_2}$ 共 $s_2$ 个数。

第 $4$ 行，为 $C_1,C_2,\ldots,C_{s_3}$ 共 $s_3$ 个数。

第 $5$ 行，为 $D_1,D_2,\ldots,D_{s_4}$ 共 $s_4$ 个数，意思均同上。

输出格式

输出一行,为复习完毕最短时间。

样例 #1

样例输入 #1

样例输出 #1

提示

$1\leq s_1,s_2,s_3,s_4\leq 20$。

$1\leq A_1,A_2,\ldots,A_{s_1},B_1,B_2,\ldots,B_{s_2},C_1,C_2,\ldots,C_{s_3},D_1,D_2,\ldots,D_{s_4}\leq60$。

题解

暴搜把每一道题分别放到左右脑之后，总时间最短的情况：

 1from functools import lru_cache
 2
 3
 4@lru_cache
 5def dfs(left: int, right: int, time: tuple):
 6    if len(time) == 0:
 7        return max(left, right)
 8
 9    return min(
10        dfs(left + time[0], right, time[1:]), dfs(left, right + time[0], time[1:])
11    )
12
13
14def main():
15    _ = input()
16    total = 0
17    for _ in range(4):
18        time = tuple(map(int, input().split()))
19        total += dfs(0, 0, time)
20    print(total)
21
22
23if __name__ == "__main__":
24    main()

这样会写会有一个点超时。因为左右脑是等价的，左右脑中的题互换时间不变，因此令每一科第一题在左脑计算，这样可以节约一半时间。

 1from functools import lru_cache
 2
 3
 4@lru_cache
 5def dfs(left: int, right: int, time: tuple):
 6    if len(time) == 0:
 7        return max(left, right)
 8
 9    return min(
10        dfs(left + time[0], right, time[1:]), dfs(left, right + time[0], time[1:])
11    )
12
13
14def main():
15    _ = input()
16    total = 0
17    for _ in range(4):
18        time = tuple(map(int, input().split()))
19        total += dfs(time[0], 0, time[1:])
20    print(total)
21
22
23if __name__ == "__main__":
24    main()

将 dfs 函数的参数 time 定义为 tuple 类型才可以开 lru_cache 优化。

[NOIP2002 普及组] 选数

题目描述

已知 $n$ 个整数 $x_1,x_2,\cdots,x_n$，以及 $1$ 个整数 $k$（$k<n$）。从 $n$ 个整数中任选 $k$ 个整数相加，可分别得到一系列的和。例如当 $n=4$，$k=3$，$4$ 个整数分别为 $3,7,12,19$ 时，可得全部的组合与它们的和为：

$3+7+12=22$

$3+7+19=29$

$7+12+19=38$

$3+12+19=34$

现在，要求你计算出和为素数共有多少种。

例如上例，只有一种的和为素数：$3+7+19=29$。

输入格式

第一行两个空格隔开的整数 $n,k$（$1 \le n \le 20$，$k<n$）。

第二行 $n$ 个整数，分别为 $x_1,x_2,\cdots,x_n$（$1 \le x_i \le 5\times 10^6$）。

输出格式

输出一个整数，表示种类数。

样例 #1

样例输入 #1

14 3
23 7 12 19

样例输出 #1

提示

【题目来源】

NOIP 2002 普及组第二题

使用深搜解决问题。因为 is_prime 函数反复调用，所以用 lru_cache 修饰器以节约时间（不加也能过）。dfs 函数没有加是因为这个修饰器要求函数参数都 hashable。

 1from functools import lru_cache
 2
 3
 4def dfs(nums, start, k, path, result):
 5    if len(path) == k:
 6        result.append(sum(path))
 7        return
 8
 9    for i in range(start, len(nums)):
10        dfs(nums, i + 1, k, path + [nums[i]], result)
11
12
13@lru_cache
14def is_prime(n):
15    if n < 2:
16        return False
17    for i in range(2, int(n**0.5) + 1):
18        if n % i == 0:
19            return False
20    return True
21
22
23def main():
24    n, k = map(int, input().split(" "))
25    nums = list(map(int, input().split(" ")))
26    result = list()
27    dfs(nums, 0, k, list(), result)
28    count = 0
29    for i in result:
30        if is_prime(i):
31            count += 1
32    print(count)
33
34
35if __name__ == "__main__":
36    main()

还可以用 itertools 模块的 combinations 函数一步到位。

 1from itertools import combinations
 2
 3
 4def isPrime(n):
 5    if n < 2:
 6        return False
 7    for i in range(2, int(n**0.5) + 1):
 8        if n % i == 0:
 9            return False
10    return True
11
12
13def main():
14    n, k = map(int, input().split(" "))
15    nums = list(map(int, input().split(" ")))
16    print(len([s for comb in combinations(nums, k) if isPrime(s := sum(comb))]))
17
18
19if __name__ == "__main__":
20    main()

时间和内存跟自己手搓的差不多。

[COCI 2008/2009 #2] PERKET

题目描述

Perket 是一种流行的美食。为了做好 Perket，厨师必须谨慎选择食材，以在保持传统风味的同时尽可能获得最全面的味道。你有 $n$ 种可支配的配料。对于每一种配料，我们知道它们各自的酸度 $s$ 和苦度 $b$。当我们添加配料时，总的酸度为每一种配料的酸度总乘积；总的苦度为每一种配料的苦度的总和。

众所周知，美食应该做到口感适中，所以我们希望选取配料，以使得酸度和苦度的绝对差最小。

另外，我们必须添加至少一种配料，因为没有任何食物以水为配料的。

输入格式

第一行一个整数 $n$，表示可供选用的食材种类数。

接下来 $n$ 行，每行 $2$ 个整数 $s_i$ 和 $b_i$，表示第 $i$ 种食材的酸度和苦度。

输出格式

一行一个整数，表示可能的总酸度和总苦度的最小绝对差。

样例 #1

样例输入 #1

11
23 10

样例输出 #1

样例 #2

样例输入 #2

12
23 8
35 8

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

提示

数据规模与约定

对于 $100%$ 的数据，有 $1 \leq n \leq 10$，且将所有可用食材全部使用产生的总酸度和总苦度小于 $1 \times 10^9$，酸度和苦度不同时为 $1$ 和 $0$。

说明

本题满分 $70$ 分。
题目译自 COCI2008-2009 CONTEST #2 PERKET，译者 @mnesia。

题解

最开始想尝试用 0-1 背包的思路来解，后来发现每一次比较的最小值不一定是最终的最小值。例如当五种调料的 s 和 b 都是 2 和 6 时，随着调料种类的增多这个差值依次是 $4\rightarrow8\rightarrow10\rightarrow8\rightarrow2$。所以还是选择用爆搜。

爆搜也有问题，就是在大多数情况下，不加任何调料，即只有初始值 s = 0, b = 1 时这个差最小。所以把所有可能出现的结果都列出来，如果结果中有 0 则输出 0，否则将结果中第二小的值输出（除了初始值 1）。

 1def dfs(s_list, b_list, current_s, current_b, index, n, result):
 2    if index == n:
 3        result.append(abs(current_s - current_b))
 4        return
 5
 6    dfs(
 7        s_list[1:],
 8        b_list[1:],
 9        current_s * s_list[0],
10        current_b + b_list[0],
11        index + 1,
12        n,
13        result,
14    )
15    dfs(s_list[1:], b_list[1:], current_s, current_b, index + 1, n, result)
16    return result
17
18
19def main():
20    n = int(input())
21    s_list, b_list = list(), list()
22    for _ in range(n):
23        s, b = map(int, input().split())
24        s_list.append(s)
25        b_list.append(b)
26    result = sorted(dfs(s_list, b_list, 1, 0, 0, n, list()))
27    if result[0]:
28        print(result[1])
29    else:
30        print(0)
31
32
33if __name__ == "__main__":
34    main()

没有 lru_cache 也能过。

迷宫

题目描述

给定一个 $N \times M$ 方格的迷宫，迷宫里有 $T$ 处障碍，障碍处不可通过。

在迷宫中移动有上下左右四种方式，每次只能移动一个方格。数据保证起点上没有障碍。

给定起点坐标和终点坐标，每个方格最多经过一次，问有多少种从起点坐标到终点坐标的方案。

输入格式

第一行为三个正整数 $N,M,T$，分别表示迷宫的长宽和障碍总数。

第二行为四个正整数 $SX,SY,FX,FY$，$SX,SY$ 代表起点坐标，$FX,FY$ 代表终点坐标。

接下来 $T$ 行，每行两个正整数，表示障碍点的坐标。

输出格式

输出从起点坐标到终点坐标的方案总数。

样例 #1

样例输入 #1

12 2 1
21 1 2 2
31 2

样例输出 #1

提示

对于 $100%$ 的数据，$1 \le N,M \le 5$，$1 \le T \le 10$，$1 \le SX,FX \le n$，$1 \le SY,FY \le m$。

题解

深搜：

 1def dfs(maze, current, dest, visited, path_count, N, M):
 2    if current == dest:
 3        path_count += 1
 4        return path_count
 5
 6    visited[current] = True
 7    x, y = current
 8
 9    if x > 1 and not visited.get((x - 1, y), False) and maze[x - 1][y]:
10        path_count = dfs(maze, (x - 1, y), dest, visited, path_count, N, M)
11    if x < N and not visited.get((x + 1, y), False) and maze[x + 1][y]:
12        path_count = dfs(maze, (x + 1, y), dest, visited, path_count, N, M)
13    if y > 1 and not visited.get((x, y - 1), False) and maze[x][y - 1]:
14        path_count = dfs(maze, (x, y - 1), dest, visited, path_count, N, M)
15    if y < M and not visited.get((x, y + 1), False) and maze[x][y + 1]:
16        path_count = dfs(maze, (x, y + 1), dest, visited, path_count, N, M)
17
18    visited[current] = False
19    return path_count
20
21
22def main():
23    N, M, T = map(int, input().strip().split(" "))
24    sx, sy, fx, fy = map(int, input().strip().split(" "))
25    maze = [[1 for _ in range(N + 1)] for _ in range(M + 1)]
26    for _ in range(T):
27        x, y = map(int, input().strip().split(" "))
28        maze[x][y] = 0
29    visited = {}
30    print(dfs(maze, (sx, sy), (fx, fy), visited, 0, N, M))
31
32
33if __name__ == "__main__":
34    main()

单词方阵

题目描述

给一 $n \times n$ 的字母方阵，内可能蕴含多个 yizhong 单词。单词在方阵中是沿着同一方向连续摆放的。摆放可沿着 $8$ 个方向的任一方向，同一单词摆放时不再改变方向，单词与单词之间可以交叉，因此有可能共用字母。输出时，将不是单词的字母用 * 代替，以突出显示单词。

输入格式

第一行输入一个数 $n$。$(7 \le n \le 100)$。

第二行开始输入 $n \times n$ 的字母矩阵。

输出格式

突出显示单词的 $n \times n$ 矩阵。

样例 #1

样例输入 #1

17
2aaaaaaa
3aaaaaaa
4aaaaaaa
5aaaaaaa
6aaaaaaa
7aaaaaaa
8aaaaaaa

样例输出 #1

1*******
2*******
3*******
4*******
5*******
6*******
7*******

样例 #2

样例输入 #2

18
2qyizhong
3gydthkjy
4nwidghji
5orbzsfgz
6hhgrhwth
7zzzzzozo
8iwdfrgng
9yyyygggg

样例输出 #2

1*yizhong
2gy******
3n*i*****
4o**z****
5h***h***
6z****o**
7i*****n*
8y******g

题解

用最朴素的方法完成。

 1def main():
 2    n = int(input())
 3    matrix = list()
 4    result = [["*" for _ in range(n)] for _ in range(n)]
 5    yizhong = "yizhong"
 6    for _ in range(n):
 7        matrix.append(list(input().strip()))
 8
 9    for i in range(n):
10        for j in range(n):
11            if matrix[i][j] == "y":
12
13                if i >= 6 and "".join(matrix[i - k][j] for k in range(7)) == yizhong:
14                    for k in range(7):
15                        result[i - k][j] = yizhong[k]
16
17                if i >= 6 and j <= n - 7 and "".join(matrix[i - k][j + k] for k in range(7)) == yizhong:
18                    for k in range(7):
19                        result[i - k][j + k] = yizhong[k]
20
21                if j <= n - 7 and "".join(matrix[i][j + k] for k in range(7)) == yizhong:
22                    for k in range(7):
23                        result[i][j + k] = yizhong[k]
24
25                if i <= n - 7 and j <= n - 7 and "".join(matrix[i + k][j + k] for k in range(7)) == yizhong:
26                    for k in range(7):
27                        result[i + k][j + k] = yizhong[k]
28
29                if i <= n - 7 and "".join(matrix[i + k][j] for k in range(7)) == yizhong:
30                    for k in range(7):
31                        result[i + k][j] = yizhong[k]
32
33                if i <= n - 7 and j >= 6 and "".join(matrix[i + k][j - k] for k in range(7)) == yizhong:
34                    for k in range(7):
35                        result[i + k][j - k] = yizhong[k]
36
37                if j >= 6 and "".join(matrix[i][j - k] for k in range(7)) == yizhong:
38                    for k in range(7):
39                        result[i][j - k] = yizhong[k]
40
41                if i >= 6 and j >= 6 and "".join(matrix[i - k][j - k] for k in range(7)) == yizhong:
42                    for k in range(7):
43                        result[i - k][j - k] = yizhong[k]
44
45    for i in range(n):
46        print("".join(result[i]))
47
48
49if __name__ == "__main__":
50    main()

自然数的拆分问题

题目描述

任何一个大于 $1$ 的自然数 $n$，总可以拆分成若干个小于 $n$ 的自然数之和。现在给你一个自然数 $n$，要求你求出 $n$ 的拆分成一些数字的和。每个拆分后的序列中的数字从小到大排序。然后你需要输出这些序列，其中字典序小的序列需要优先输出。

输入格式

输入：待拆分的自然数 $n$。

输出格式

输出：若干数的加法式子。

样例 #1

样例输入 #1

样例输出 #1

 11+1+1+1+1+1+1
 21+1+1+1+1+2
 31+1+1+1+3
 41+1+1+2+2
 51+1+1+4
 61+1+2+3
 71+1+5
 81+2+2+2
 91+2+4
101+3+3
111+6
122+2+3
132+5
143+4

提示

数据保证，$2\leq n\le 8$。

题解

简单递归

 1def dfs(current_nums, current_sum, n, result, start):
 2    if current_sum == n:
 3        result.append("+".join(current_nums))
 4        return result
 5
 6    for i in range(start, n - current_sum + 1):
 7        dfs(current_nums + [str(i)], current_sum + i, n, result, i)
 8
 9    return result
10
11
12def main():
13    n = int(input())
14    result = dfs(list(), 0, n, list(), 1)
15    print(*result[:-1], sep="\n")
16
17
18if __name__ == "__main__":
19    main()

[USACO10OCT] Lake Counting S

题面翻译

由于近期的降雨，雨水汇集在农民约翰的田地不同的地方。我们用一个 $N\times M(1\leq N\leq 100, 1\leq M\leq 100)$ 的网格图表示。每个网格中有水（W）或是旱地（.）。一个网格与其周围的八个网格相连，而一组相连的网格视为一个水坑。约翰想弄清楚他的田地已经形成了多少水坑。给出约翰田地的示意图，确定当中有多少水坑。

输入第 $1$ 行：两个空格隔开的整数：$N$ 和 $M$。

第 $2$ 行到第 $N+1$ 行：每行 $M$ 个字符，每个字符是 W 或 .，它们表示网格图中的一排。字符之间没有空格。

输出一行，表示水坑的数量。

题目描述

Due to recent rains, water has pooled in various places in Farmer John's field, which is represented by a rectangle of N x M (1 <= N <= 100; 1 <= M <= 100) squares. Each square contains either water ('W') or dry land ('.'). Farmer John would like to figure out how many ponds have formed in his field. A pond is a connected set of squares with water in them, where a square is considered adjacent to all eight of its neighbors. Given a diagram of Farmer John's field, determine how many ponds he has.

输入格式

Line 1: Two space-separated integers: N and M * Lines 2..N+1: M characters per line representing one row of Farmer John's field. Each character is either 'W' or '.'. The characters do not have spaces between them.

输出格式

Line 1: The number of ponds in Farmer John's field.

样例 #1

样例输入 #1

 110 12
 2W........WW.
 3.WWW.....WWW
 4....WW...WW.
 5.........WW.
 6.........W..
 7..W......W..
 8.W.W.....WW.
 9W.W.W.....W.
10.W.W......W.
11..W.......W.

样例输出 #1

提示

OUTPUT DETAILS: There are three ponds: one in the upper left, one in the lower left, and one along the right side.

题解

这道题的数据给的比较极限，用广搜做的话要么会 TLE 要么会 MLE，要么两者都有。

 1from collections import deque
 2import sys
 3
 4
 5def bfs(field, queue, n, m):
 6    while queue:
 7        x, y = queue.popleft()
 8        field[x][y] = "."
 9        if x > 0 and field[x - 1][y] == "W":
10            queue.append((x - 1, y))
11        if x > 0 and y < m - 1 and field[x - 1][y + 1] == "W":
12            queue.append((x - 1, y + 1))
13        if y < m - 1 and field[x][y + 1] == "W":
14            queue.append((x, y + 1))
15        if x < n - 1 and y < m - 1 and field[x + 1][y + 1] == "W":
16            queue.append((x + 1, y + 1))
17        if x < n - 1 and field[x + 1][y] == "W":
18            queue.append((x + 1, y))
19        if x < n - 1 and y > 0 and field[x + 1][y - 1] == "W":
20            queue.append((x + 1, y - 1))
21        if y > 0 and field[x][y - 1] == "W":
22            queue.append((x, y - 1))
23        if x > 0 and y > 0 and field[x - 1][y - 1] == "W":
24            queue.append((x - 1, y - 1))
25
26
27def main():
28    data = sys.stdin.read().splitlines()
29    n, m = map(int, data[0].split(" "))
30    field = list()
31    for i in range(n):
32        field.append(list(data[i + 1].strip()))
33
34    count = 0
35    queue = deque()
36    for i in range(n):
37        for j in range(m):
38            if field[i][j] == "W":
39                queue.append((i, j))
40                bfs(field, queue, n, m)
41                count += 1
42    print(count)
43
44
45if __name__ == "__main__":
46    main()

 1import java.util.Scanner;
 2import java.util.Queue;
 3import java.util.LinkedList;
 4
 5public class Main {
 6    public static void main(String[] args) {
 7        Scanner scanner = new Scanner(System.in);
 8        int n = scanner.nextInt();
 9        int m = scanner.nextInt();
10        scanner.nextLine();
11        char[][] field = new char[n][m];
12        for (int i = 0; i < n; i++) {
13            field[i] = scanner.nextLine().trim().toCharArray();
14        }
15        scanner.close();
16
17        int count = 0;
18        Queue<int[]> queue = new LinkedList<>();
19        for (int i = 0; i < n; i++) {
20            for (int j = 0; j < m; j++) {
21                if (field[i][j] == 'W') {
22                    queue.add(new int[] { i, j });
23                    bfs(field, queue, n, m);
24                    count++;
25                }
26            }
27        }
28        System.out.println(count);
29    }
30
31    public static void bfs(char[][] field, Queue<int[]> queue, int n, int m) {
32        int[] location;
33        int x, y, dx, dy;
34        int[][] directions = { { -1, 0 }, { -1, 1 }, { 0, 1 }, { 1, 1 }, { 1, 0 }, { 1, -1 }, { 0, -1 }, { -1, -1 } };
35        while (!queue.isEmpty()) {
36            location = queue.poll();
37            x = location[0];
38            y = location[1];
39            field[x][y] = '.';
40
41            for (int[] d : directions) {
42                dx = d[0];
43                dy = d[1];
44
45                if (x + dx >= 0 && x + dx < n && y + dy >= 0 && y + dy < m && field[x + dx][y + dy] == 'W') {
46                    queue.add(new int[] { x + dx, y + dy });
47                }
48            }
49        }
50    }
51}

 1#define _CRT_SECURE_NO_WARNINGS
 2
 3#include <cstdio>
 4#include <queue>
 5#include <vector>
 6    
 7using namespace std;
 8
 9vector<pair<int, int>> directions = { {-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1} };
10char line[105];
11int i, j;
12
13void bfs(vector<vector<char>>& field, queue<pair<int, int>>& q, int n, int m) {
14    int x, y, dx, dy;
15    while (!q.empty()) {
16        pair<int, int> location = q.front();
17        q.pop();
18        x = location.first;
19        y = location.second;
20        field[x][y] = '.';
21
22        for (const auto& d : directions) {
23            dx = d.first;
24            dy = d.second;
25
26            if (x + dx >= 0 && x + dx < n && y + dy >= 0 && y + dy < m && field[x + dx][y + dy] == 'W') {
27                q.push({ x + dx, y + dy });
28            }
29        }
30    }
31}
32
33int main() {
34    int n, m;
35    scanf("%d %d", &n, &m);
36
37    vector<vector<char>> field(n, vector<char>(m));
38    for (i = 0; i < n; i++) {
39        scanf("%s", line);
40        for (j = 0; line[j] != '\0'; j++) {
41            field[i][j] = line[j];
42        }
43    }
44
45    int count = 0;
46    queue<pair<int, int>> q;
47    for (i = 0; i < n; i++) {
48        for (j = 0; j < m; j++) {
49            if (field[i][j] == 'W') {
50                q.push({ i, j });
51                bfs(field, q, n, m);
52                count++;
53            }
54        }
55    }
56    printf("%d\n", count);
57    return 0;
58}

以上三个都用了广搜做，结果都没有 AC。下面是使用深搜 AC 的代码：

 1import sys
 2
 3sys.setrecursionlimit(10000)
 4
 5
 6def dfs(field, x, y, n, m):
 7    directions = [(-1, 0), (-1, 1), (0, 1), (1, 1), (1, 0), (1, -1), (0, -1), (-1, -1)]
 8    field[x][y] = "."
 9    for dx, dy in directions:
10        nx, ny = x + dx, y + dy
11        if 0 <= nx < n and 0 <= ny < m and field[nx][ny] == "W":
12            dfs(field, nx, ny, n, m)
13
14
15def main():
16    data = sys.stdin.read().splitlines()
17    n, m = map(int, data[0].split(" "))
18    field = list()
19    for i in range(n):
20        field.append(list(data[i + 1].strip()))
21
22    count = 0
23    for i in range(n):
24        for j in range(m):
25            if field[i][j] == "W":
26                dfs(field, i, j, n, m)
27                count += 1
28    print(count)
29
30
31if __name__ == "__main__":
32    main()

有一个测试点的数据是 n = 100, m = 100 且所有点都是 W。没有 sys.setrecursionlimit(10000) 就会抛出 RecursionError: maximum recursion depth exceeded。

填涂颜色

题目描述

由数字 $0$ 组成的方阵中，有一任意形状的由数字 $1$ 构成的闭合圈。现要求把闭合圈内的所有空间都填写成 $2$。例如：$6\times 6$ 的方阵（$n=6$），涂色前和涂色后的方阵如下：

如果从某个 $0$ 出发，只向上下左右 $4$ 个方向移动且仅经过其他 $0$ 的情况下，无法到达方阵的边界，就认为这个 $0$ 在闭合圈内。闭合圈不一定是环形的，可以是任意形状，但保证闭合圈内的 $0$ 是连通的（两两之间可以相互到达）。

10 0 0 0 0 0
20 0 0 1 1 1
30 1 1 0 0 1
41 1 0 0 0 1
51 0 0 1 0 1
61 1 1 1 1 1

10 0 0 0 0 0
20 0 0 1 1 1
30 1 1 2 2 1
41 1 2 2 2 1
51 2 2 1 2 1
61 1 1 1 1 1

输入格式

每组测试数据第一行一个整数 $n(1 \le n \le 30)$。

接下来 $n$ 行，由 $0$ 和 $1$ 组成的 $n \times n$ 的方阵。

方阵内只有一个闭合圈，圈内至少有一个 $0$。

输出格式

已经填好数字 $2$ 的完整方阵。

样例 #1

样例输入 #1

16
20 0 0 0 0 0
30 0 1 1 1 1
40 1 1 0 0 1
51 1 0 0 0 1
61 0 0 0 0 1
71 1 1 1 1 1

样例输出 #1

10 0 0 0 0 0
20 0 1 1 1 1
30 1 1 2 2 1
41 1 2 2 2 1
51 2 2 2 2 1
61 1 1 1 1 1

提示

对于 $100%$ 的数据，$1 \le n \le 30$。

题解

和上一道题一样，这也是一道找联通块的问题。可以在读取时将全部 0 都转换为 2，随后从边界开始搜索，能搜索到的改成 0，剩下的就是和边界不连通的。

 1from collections import deque
 2
 3
 4def bfs(graph, n, queue):
 5    directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]
 6    while queue:
 7        x, y = queue.popleft()
 8        graph[x][y] = "0"
 9        for dx, dy in directions:
10            nx, ny = x + dx, y + dy
11            if 0 <= nx < n and 0 <= ny < n and graph[nx][ny] == "2":
12                queue.append((nx, ny))
13
14
15def main():
16    n = int(input())
17    graph = list()
18    for _ in range(n):
19        graph.append(
20            list(map(lambda x: "2" if x == "0" else "1", input().strip().split(" ")))
21        )
22
23    queue = deque()
24    for i in range(n):
25        if graph[0][i] == "2":
26            queue.append((0, i))
27            bfs(graph, n, queue)
28        if graph[-1][i] == "2":
29            queue.append((n - 1, i))
30            bfs(graph, n, queue)
31        if graph[i][0] == "2":
32            queue.append((i, 0))
33            bfs(graph, n, queue)
34        if graph[i][-1] == "2":
35            queue.append((i, n - 1))
36            bfs(graph, n, queue)
37
38    print(*list(" ".join(x) for x in graph), sep="\n")
39
40
41if __name__ == "__main__":
42    main()

[USACO1.5] 八皇后 Checker Challenge

题目描述

一个如下的 $6 \times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

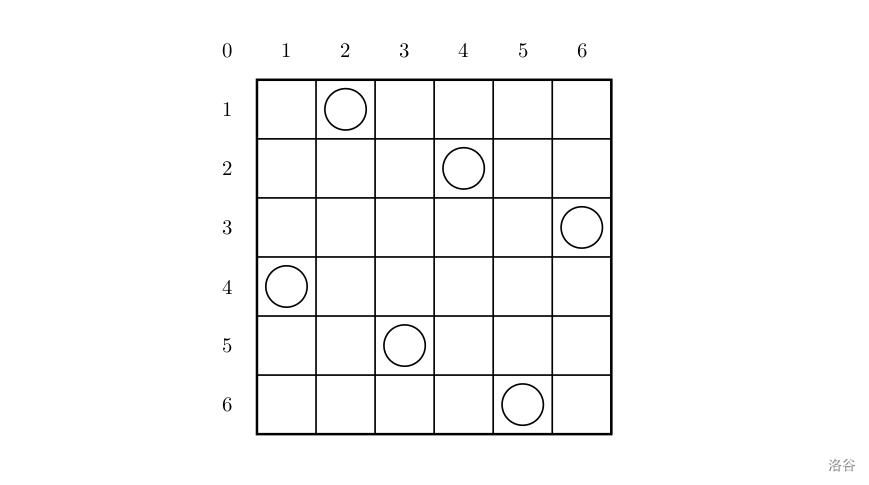
上面的布局可以用序列 $2\ 4\ 6\ 1\ 3\ 5$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $1\ 2\ 3\ 4\ 5\ 6$

列号 $2\ 4\ 6\ 1\ 3\ 5$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。并把它们以上面的序列方法输出，解按字典顺序排列。请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n \times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

样例 #1

样例输入 #1

样例输出 #1

12 4 6 1 3 5
23 6 2 5 1 4
34 1 5 2 6 3
44

提示

【数据范围】对于 $100%$ 的数据，$6 \le n \le 13$。

题目翻译来自NOCOW。

USACO Training Section 1.5

题解

遍历一行的每一个格子，判断这个格子是否能放棋子。如果可以放，则放棋子并标记，然后进入下一行遍历。

行和列比较好标记：因为将上一行的棋子放下后才能在下一行继续放棋子，所以行不可能重复；列只要把列号标记就好了。比较困难的是给对角线和副对角线标记。观察发现，对于同一条对角线上的坐标 (i, j)，i - j 是相等的；对于同一条副对角线上的坐标 (i, j)，i + j 是相等的（就是一次函数）。

 1#define _CRT_SECURE_NO_WARNINGS
 2
 3#include <cstdio>
 4#include <vector>
 5
 6using namespace std;
 7
 8int cols[14] = { 0 }, main_diag[25] = { 0 }, anti_diag[25] = { 0 };
 9
10void dfs(int n, int row, vector<int> &current, vector<vector<int>> &result) {
11    if (row == n + 1) {
12        result.push_back(current);
13        return;
14    }
15
16    for (int col = 1; col <= n; col++) {
17        if (cols[col] == 0 && main_diag[col - row + n] == 0 && anti_diag[col + row - 1] == 0) {
18            cols[col] = 1;
19            main_diag[col - row + n] = 1;
20            anti_diag[col + row - 1] = 1;
21            current.push_back(col);
22            dfs(n, row + 1, current, result);
23            current.pop_back();
24            cols[col] = 0;
25            main_diag[col - row + n] = 0;
26            anti_diag[col + row - 1] = 0;
27        }
28    }
29}
30
31int main() {
32    int n;
33    scanf("%d", &n);
34    vector<int> current;
35    vector<vector<int>> result;
36    dfs(n, 1, current, result);
37    for (int i = 0; i < 3; i++) {
38        for (const auto& num : result[i]) {
39            printf("%d ", num);
40        }
41        printf("\n");
42    }
43    printf("%d\n", result.size());
44    return 0;
45}

马的遍历

题目描述

有一个 $n \times m$ 的棋盘，在某个点 $(x, y)$ 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

输入格式

输入只有一行四个整数，分别为 $n, m, x, y$。

输出格式

一个 $n \times m$ 的矩阵，代表马到达某个点最少要走几步（不能到达则输出 $-1$）。

样例 #1

样例输入 #1

13 3 1 1

样例输出 #1

10    3    2
23    -1   1
32    1    4

提示

数据规模与约定

对于全部的测试点，保证 $1 \leq x \leq n \leq 400$，$1 \leq y \leq m \leq 400$。

题解

这道题本质上也是一个洪水填充，只是每次移动的方向不一样。使用广搜解决，第一次到达某一点时的步数即为最少步数。求某两点之间的最短步数也是相同解法。

 1#include <iostream>
 2#include <queue>
 3
 4using namespace std;
 5
 6int field[405][405];
 7int n, m, x_0, y_0;
 8const int directions[16] = { -2, 1, -1, 2, 1, 2, 2, 1, 2, -1, 1, -2, -1, -2, -2, -1 };
 9int i;
10
11void bfs() {
12    queue<pair<int, int>> q;
13    q.push(make_pair(x_0 - 1, y_0 - 1));
14    field[x_0 - 1][y_0 - 1] = 0;
15    int x, y, nx, ny;
16    while (!q.empty()) {
17        x = q.front().first;
18        y = q.front().second;
19        q.pop();
20
21        for (i = 0; i < 16; i += 2) {
22            nx = x + directions[i];
23            ny = y + directions[i + 1];
24            if (nx >= 0 && nx < n && ny >= 0 && ny < m && field[nx][ny] == -1) {
25                q.push(make_pair(nx, ny));
26                field[nx][ny] = field[x][y] + 1;
27            }
28        }
29    }
30}
31
32int main() {
33    cin >> n >> m >> x_0 >> y_0;
34    for (int i = 0; i < n; i++) {
35        for (int j = 0; j < m; j++) {
36            field[i][j] = -1;
37        }
38    }
39
40    bfs();
41
42    for (int i = 0; i < n; i++) {
43        for (int j = 0; j < m; j++) {
44            cout << field[i][j] << "\t";
45        }
46        cout << endl;
47    }
48    return 0;
49}

奇怪的电梯

题目背景

感谢 @yummy 提供的一些数据。

题目描述

呵呵，有一天我做了一个梦，梦见了一种很奇怪的电梯。大楼的每一层楼都可以停电梯，而且第 $i$ 层楼（$1 \le i \le N$）上有一个数字 $K_i$（$0 \le K_i \le N$）。电梯只有四个按钮：开，关，上，下。上下的层数等于当前楼层上的那个数字。当然，如果不能满足要求，相应的按钮就会失灵。例如： $3, 3, 1, 2, 5$ 代表了 $K_i$（$K_1=3$，$K_2=3$，……），从 $1$ 楼开始。在 $1$ 楼，按“上”可以到 $4$ 楼，按“下”是不起作用的，因为没有 $-2$ 楼。那么，从 $A$ 楼到 $B$ 楼至少要按几次按钮呢？

输入格式

共二行。

第一行为三个用空格隔开的正整数，表示 $N, A, B$（$1 \le N \le 200$，$1 \le A, B \le N$）。

第二行为 $N$ 个用空格隔开的非负整数，表示 $K_i$。

输出格式

一行，即最少按键次数，若无法到达，则输出 -1。

样例 #1

样例输入 #1

15 1 5
23 3 1 2 5

样例输出 #1

提示

对于 $100 %$ 的数据，$1 \le N \le 200$，$1 \le A, B \le N$，$0 \le K_i \le N$。

本题共 $16$ 个测试点，前 $15$ 个每个测试点 $6$ 分，最后一个测试点 $10$ 分。

题解

这道题和上一道题几乎一模一样，最容易想到的办法是使用广搜找出最短路径。然而这道题给了些极限数据，使用广搜会 MLE，用一般的深搜会超时，所以不得不用深搜记忆化搜索和剪枝来解决。

 1import sys
 2from functools import lru_cache
 3
 4sys.setrecursionlimit(10000)
 5
 6
 7def main():
 8    input = sys.stdin.read
 9    data = input().split()
10
11    N = int(data[0])
12    A = int(data[1])
13    B = int(data[2])
14    K = (0,) + tuple(map(int, data[3 : 3 + N]))
15    memo = {}
16    visited = [False] * (N + 1)
17
18    @lru_cache
19    def dfs(current, depth):
20        if current == B:
21            return depth
22        if K[current] == 0:
23            return float("inf")
24        if current in memo and memo[current] <= depth:
25            return float("inf")
26
27        memo[current] = depth
28        min_depth = float("inf")
29
30        up = current + K[current]
31        if 1 <= up <= N and not visited[up]:
32            visited[up] = True
33            result = dfs(up, depth + 1)
34            min_depth = min(min_depth, result)
35            visited[up] = False
36        down = current - K[current]
37        if 1 <= down <= N and not visited[down]:
38            visited[down] = True
39            result = dfs(down, depth + 1)
40            min_depth = min(min_depth, result)
41            visited[down] = False
42
43        return min_depth
44
45    visited[A] = True
46    result = dfs(A, 0)
47    print(result if result != float("inf") else -1)
48
49
50if __name__ == "__main__":
51    main()

[USACO08FEB] Meteor Shower S

题面翻译

题目描述

贝茜听说一场特别的流星雨即将到来：这些流星会撞向地球，并摧毁它们所撞击的任何东西。她为自己的安全感到焦虑，发誓要找到一个安全的地方（一个永远不会被流星摧毁的地方）。

如果将牧场放入一个直角坐标系中，贝茜现在的位置是原点，并且，贝茜不能踏上一块被流星砸过的土地。

根据预报，一共有 $M$ 颗流星 $(1\leq M\leq 50,000)$ 会坠落在农场上，其中第 $i$ 颗流星会在时刻 $T_i$（$0 \leq T _ i \leq 1000$）砸在坐标为 $(X_i,Y_i)(0\leq X_i\leq 300$，$0\leq Y_i\leq 300)$ 的格子里。流星的力量会将它所在的格子，以及周围 $4$ 个相邻的格子都化为焦土，当然贝茜也无法再在这些格子上行走。

贝茜在时刻 $0$ 开始行动，她只能在会在横纵坐标 $X,Y\ge 0$ 的区域中，平行于坐标轴行动，每 $1$ 个时刻中，她能移动到相邻的（一般是 $4$ 个）格子中的任意一个，当然目标格子要没有被烧焦才行。如果一个格子在时刻 $t$ 被流星撞击或烧焦，那么贝茜只能在 $t$ 之前的时刻在这个格子里出现。贝茜一开始在 $(0,0)$。

请你计算一下，贝茜最少需要多少时间才能到达一个安全的格子。如果不可能到达输出 $−1$。

输入格式

共 $M+1$ 行，第 $1$ 行输入一个整数 $M$，接下来的 $M$ 行每行输入三个整数分别为 $X_i, Y_i, T_i$。

输出格式

贝茜到达安全地点所需的最短时间，如果不可能，则为 $-1$。

题目描述

Bessie hears that an extraordinary meteor shower is coming; reports say that these meteors will crash into earth and destroy anything they hit. Anxious for her safety, she vows to find her way to a safe location (one that is never destroyed by a meteor) . She is currently grazing at the origin in the coordinate plane and wants to move to a new, safer location while avoiding being destroyed by meteors along her way.

The reports say that M meteors (1 ≤ M ≤ 50,000) will strike, with meteor i will striking point (Xi, Yi) (0 ≤ Xi ≤ 300; 0 ≤ Yi ≤ 300) at time Ti (0 ≤ Ti ≤ 1,000). Each meteor destroys the point that it strikes and also the four rectilinearly adjacent lattice points.

Bessie leaves the origin at time 0 and can travel in the first quadrant and parallel to the axes at the rate of one distance unit per second to any of the (often 4) adjacent rectilinear points that are not yet destroyed by a meteor. She cannot be located on a point at any time greater than or equal to the time it is destroyed).

Determine the minimum time it takes Bessie to get to a safe place.

输入格式

* Line 1: A single integer: M

* Lines 2..M+1: Line i+1 contains three space-separated integers: Xi, Yi, and Ti

输出格式

* Line 1: The minimum time it takes Bessie to get to a safe place or -1 if it is impossible.

样例 #1

样例输入 #1

样例输出 #1

题解

创建 meteor 数组用于保存每一个点无法通行的时间，field 数组用于保存到达每一点的最短时间。只有当节点没有走过而且还没有被摧毁时才可以通行。依然使用深搜找出最短路径。

 1#define _CRT_SECURE_NO_WARNINGS
 2
 3#include <cstdio>
 4#include <algorithm>
 5#include <queue>
 6
 7using namespace std;
 8
 9const int INF = 1e9;
10const int directions[8] = { 0, 1, 1, 0, 0, -1, -1, 0 };
11int meteor[305][305], field[305][305] = {};
12int n, xi, yi, ti, nxi, nyi, x, y, nx, ny;
13int i, j;
14
15int main() {
16    for (i = 0; i < 305; i++) {
17        for (j = 0; j < 305; j++) {
18            meteor[i][j] = INF;
19        }
20    }
21
22    scanf("%d", &n);
23    for (i = 0; i < n; i++) {
24        scanf("%d%d%d", &xi, &yi, &ti);
25        meteor[xi][yi] = min(meteor[xi][yi], ti);
26        for (j = 0; j < 8; j += 2) {
27            nxi = xi + directions[j];
28            nyi = yi + directions[j + 1];
29            if (nxi >= 0 && nyi >= 0) {
30                meteor[nxi][nyi] = min(meteor[nxi][nyi], ti);
31            }
32        }
33    }
34
35    queue<int> q;
36    q.push(0);
37    q.push(0);
38
39    while (!q.empty()) {
40        x = q.front();
41        q.pop();
42        y = q.front();
43        q.pop();
44
45        if (meteor[x][y] == INF) {
46            printf("%d", field[x][y]);
47            return 0;
48        }
49
50        for (i = 0; i < 8; i += 2) {
51            nx = x + directions[i];
52            ny = y + directions[i + 1];
53            if (nx >= 0 && ny >= 0 && field[x][y] + 1 < meteor[nx][ny] && !field[nx][ny]) {
54                q.push(nx);
55                q.push(ny);
56                field[nx][ny] = field[x][y] + 1;
57            }
58        }
59    }
60
61    puts("-1");
62    return 0;
63}

至少在 C++ 中，避免向 queue 中存储过多数据可以极大降低程序运行所花费的时间和空间。最开始我尝试将经过某一点时的坐标和时间同时存入队列，导致部分测试点 MLE 或 TLE。后来单独使用二维数组存储时间，将每组存入队列的数据从三个减少到两个才可以 AC。

[NOIP 2000 提高组] 单词接龙

题目背景

注意：本题为上古 NOIP 原题，不保证存在靠谱的做法能通过该数据范围下的所有数据。

本题为搜索题，本题不接受 hack 数据。关于此类题目的详细内容

NOIP2000 提高组 T3

题目描述

单词接龙是一个与我们经常玩的成语接龙相类似的游戏，现在我们已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”（每个单词都最多在“龙”中出现两次），在两个单词相连时，其重合部分合为一部分，例如 beast 和 astonish，如果接成一条龙则变为 beastonish，另外相邻的两部分不能存在包含关系，例如 at 和 atide 间不能相连。

输入格式

输入的第一行为一个单独的整数 $n$ 表示单词数，以下 $n$ 行每行有一个单词，输入的最后一行为一个单个字符，表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在。

输出格式

只需输出以此字母开头的最长的“龙”的长度。

样例 #1

样例输入 #1

15
2at
3touch
4cheat
5choose
6tact
7a

样例输出 #1

提示

样例解释：连成的“龙”为 atoucheatactactouchoose。

$n \le 20$。

题解

数据很水，只要把各种限制条件和特判加上，这样乱写也能 AC。

 1def main():
 2    n = int(input().strip())
 3    rest = dict()
 4    for _ in range(n):
 5        word = input().strip()
 6        rest[word] = 2
 7    start = input().strip()
 8    result = set()
 9
10    def dfs(cur, ln):
11        result.add(cur)
12
13        if ln == 1:
14            for w in rest.keys():
15                if w[0] == cur:
16                    rest[w] -= 1
17                    nxt = w
18                    dfs(nxt, len(nxt))
19                    rest[w] += 1
20
21        else:
22            for w in rest.keys():
23                if rest[w]:
24                    rest[w] -= 1
25                    for i in range(1, min(ln, len(w))):
26                        if cur[ln - i :] == w[:i]:
27                            nxt = cur + w[i:]
28                            dfs(nxt, len(nxt))
29                    rest[w] += 1
30
31    dfs(start, 1)
32    result = list(result)
33    result.sort(key=lambda x: len(x), reverse=True)
34    print(len(result[0]))
35
36
37if __name__ == "__main__":
38    main()

[USACO11OPEN] Corn Maze S

题面翻译

奶牛们去一个 $N\times M$ 玉米迷宫，$2 \leq N \leq 300,2 \leq M \leq300$。

迷宫里有一些传送装置，可以将奶牛从一点到另一点进行瞬间转移。这些装置可以双向使用。

如果一头奶牛处在这个装置的起点或者终点，这头奶牛就必须使用这个装置，奶牛在传送过后不会立刻进行第二次传送，即不会卡在传送装置的起点和终点之间来回传送。

玉米迷宫除了唯一的一个出口都被玉米包围。

迷宫中的每个元素都由以下项目中的一项组成：

玉米，# 表示，这些格子是不可以通过的。
草地，. 表示，可以简单的通过。
传送装置，每一对大写字母 $\tt{A}$ 到 $\tt{Z}$ 表示。
出口，= 表示。
起点， @ 表示

奶牛能在一格草地上可能存在的四个相邻的格子移动，花费 $1$ 个单位时间。从装置的一个结点到另一个结点不花时间。

题目描述

This past fall, Farmer John took the cows to visit a corn maze. But this wasn't just any corn maze: it featured several gravity-powered teleporter slides, which cause cows to teleport instantly from one point in the maze to another. The slides work in both directions: a cow can slide from the slide's start to the end instantly, or from the end to the start. If a cow steps on a space that hosts either end of a slide, she must use the slide.

The outside of the corn maze is entirely corn except for a single exit.

The maze can be represented by an N x M (2 <= N <= 300; 2 <= M <= 300) grid. Each grid element contains one of these items:

* Corn (corn grid elements are impassable)

* Grass (easy to pass through!)

* A slide endpoint (which will transport a cow to the other endpoint)

* The exit

A cow can only move from one space to the next if they are adjacent and neither contains corn. Each grassy space has four potential neighbors to which a cow can travel. It takes 1 unit of time to move from a grassy space to an adjacent space; it takes 0 units of time to move from one slide endpoint to the other.

Corn-filled spaces are denoted with an octothorpe (#). Grassy spaces are denoted with a period (.). Pairs of slide endpoints are denoted with the same uppercase letter (A-Z), and no two different slides have endpoints denoted with the same letter. The exit is denoted with the equals sign (=).

Bessie got lost. She knows where she is on the grid, and marked her current grassy space with the 'at' symbol (@). What is the minimum time she needs to move to the exit space?

输入格式

第一行：两个用空格隔开的整数 $N$ 和 $M$。

第 $2\sim N+1$ 行：第 $i+1$ 行描述了迷宫中的第 $i$ 行的情况（共有$M$个字符，每个字符中间没有空格）。

输出格式

一个整数，表示起点到出口所需的最短时间。

样例 #1

样例输入 #1

15 6
2###=##
3#.W.##
4#.####
5#.@W##
6######

样例输出 #1

提示

例如以下矩阵，$N=5,M=6$。

1###=##
2#.W.##
3#.####
4#.@W##
5######

唯一的一个装置的结点用大写字母 $\tt{W}$ 表示。

最优方案为：先向右走到装置的结点，花费一个单位时间，再到装置的另一个结点上，花费 $0$ 个单位时间，然后再向右走一个，再向上走一个，到达出口处，总共花费了 $3$ 个单位时间。

题解

这道题本质上还是一个广搜走迷宫的问题，只是加了传送门需要特判。传送门可以传送过去，也可以传送回来，而且一对传送门可以重复使用。例如下面这种情况：

1####=#
2#....#
3#.####
4#.#A.#
5#.####
6#.A.@#
7######

因为传送本身不计算步数，所以穿过传送门时增加的步数应该记在出口传送门上，这样防止反复穿越传送门时错误地计算步数。

 1from collections import deque
 2
 3
 4def main():
 5    portal = dict()
 6    n, m = map(int, input().strip().split(" "))
 7    maze = list()
 8    visited = [[-1 for _ in range(m)] for _ in range(n)]
 9    for i in range(n):
10        row = list(input().strip())
11        maze.append(row)
12        for j in range(m):
13            if row[j] == "@":
14                start = (i, j)
15            elif row[j].isalpha():
16                p = portal.get(row[j], list())
17                p.append((i, j))
18                portal[row[j]] = p
19
20    sx, sy = start
21    visited[sx][sy] = 0
22    directions = ((-1, 0), (0, 1), (1, 0), (0, -1))
23    q = deque()
24    q.append(start)
25
26    while q:
27        x, y = q.popleft()
28
29        for dx, dy in directions:
30            nx, ny = x + dx, y + dy
31            if maze[nx][ny] == "=":
32                print(visited[x][y] + 1)
33                return
34            elif maze[nx][ny] == "." and visited[nx][ny] == -1:
35                q.append((nx, ny))
36                visited[nx][ny] = visited[x][y] + 1
37            elif maze[nx][ny].isalpha():
38                if portal[maze[nx][ny]][0] != (nx, ny):
39                    px, py = portal[maze[nx][ny]][0]
40                else:
41                    px, py = portal[maze[nx][ny]][1]
42
43                if visited[px][py] == -1:
44                    q.append((px, py))
45                    visited[px][py] = visited[x][y] + 1
46
47
48if __name__ == "__main__":
49    main()